Indholdsfortegnelse:
Video: Hvordan finder du faste omkostninger ved hjælp af mindste kvadraters regression?

2024 Forfatter: Stanley Ellington | [email protected]. Sidst ændret: 2024-01-18 08:16
Beregning af samlede faste omkostninger (a):
- Ved brug af det metode af mindste kvadrater , det koste Funktionen af Master Chemicals er: y = $14, 620 + $11,77x.
- Det samlede beløb koste ved et aktivitetsniveau på 6.000 flasker: y = $14.620 + ($11.77 × 6.000) = $85.240.
- Det samlede beløb koste ved et aktivitetsniveau på 12.000 flasker: y = $14.620 + ($11.77 × 12.000)
Og hvordan beregner du mindste kvadraters regression?
Trin
- Trin 1: Beregn x for hvert (x, y) punkt2 og xy.
- Trin 2: Sum alle x, y, x2 og xy, som giver os Σx, Σy, Σx2 og Σxy (Σ betyder "sum op")
- Trin 3: Beregn hældning m:
- m = N Σ(xy) − Σx Σy N Σ(x2) − (Σx)2
- Trin 4: Beregn skæringspunkt b:
- b = Σy − m Σx N.
- Trin 5: Saml ligningen for en linje.
hvad er meningen med mindste kvadrater i en regressionsmodel? Det Mindste kvadraters regression Linje er den linje, der gør den lodrette afstand fra datapunkterne til regression linje så lille som muligt. Det kaldes en mindste kvadrater ” fordi den bedste tilpasningslinje er en, der minimerer variansen (summen af firkanter af fejlene).
Derfor, hvordan bruger du mindste kvadraters metode?
Det metode af mindste kvadrater antager, at den bedst tilpassede kurve af en given type er den kurve, der har den minimale sum af afvigelser, dvs. mindst kvadratisk fejl fra et givet datasæt. Ifølge metode af mindste kvadrater , den bedst passende kurve har den egenskab, at ∑ 1 n e i 2 = ∑ 1 n [y i − f (x i)] 2 er minimum.
I hvilken tilgang til omkostningsestimering anvendes mindste kvadrater?
Det mindst - kvadratmetode til omkostningsberegning involverer brug af matematiske regressionsteknikker til at beregne hældningen og skæringspunktet for den bedst tilpassede linje for anvendte omkostninger i skøn . For at bestemme disse estimater vil en leder samles koste data af koste og produktionsniveau.
Anbefalede:
Hvordan finder du enhedsproduktomkostningerne ved hjælp af traditionel efterregning?

Saml dine samlede direkte materialeromkostninger, dine samlede direkte lønomkostninger og dine samlede produktionsomkostninger, du har afholdt i perioden for at bestemme dine samlede produktomkostninger. Divider dit resultat med antallet af produkter, du har fremstillet i løbet af perioden for at bestemme din produktpris pr. enhed
Er faste omkostninger altid faste?

Faste omkostninger er i modsætning til variable omkostninger, som stiger eller falder med virksomhedens produktions- eller forretningsaktivitet. Tilsammen udgør faste omkostninger og variable omkostninger de samlede produktionsomkostninger. En fast omkostning forbliver ikke nødvendigvis helt konstant. Det kan variere
Kan faste omkostninger blive til variable omkostninger?
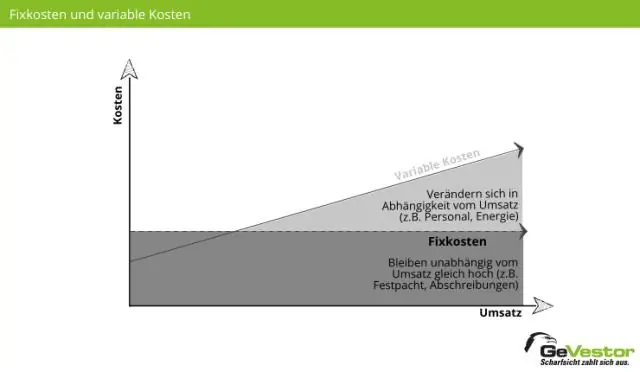
Samlede omkostninger er summen af faste og variable omkostninger. Variable omkostninger ændres i overensstemmelse med mængden af en vare eller tjenesteydelse, der produceres. Faste omkostninger er kun kortsigtede og ændrer sig over tid. Det lange løb er tilstrækkelig tid af alle kortsigtede input, der er fikseret til at blive variable
Hvad er faste omkostninger og variable omkostninger i økonomi?

Inden for økonomi er variable omkostninger og faste omkostninger de to vigtigste omkostninger, en virksomhed har, når de producerer varer og tjenester. En variabel omkostning varierer med den producerede mængde, mens en fast omkostning forbliver den samme, uanset hvor meget output en virksomhed producerer
Hvad er forskellen mellem faste omkostninger og variable omkostninger?

Variable omkostninger varierer baseret på mængden af output, mens faste omkostninger er de samme uanset produktionsoutput. Eksempler på variable omkostninger omfatter arbejdskraft og omkostninger til råvarer, mens faste omkostninger kan omfatte leasing- og lejebetalinger, forsikringer og rentebetalinger
