
Video: Hvad er Eulers formel ved at bruge antallet af flader af tetraeder med toppunkter som 4 og 6 kanter?
2024 Forfatter: Stanley Ellington | [email protected]. Sidst ændret: 2023-12-16 00:15
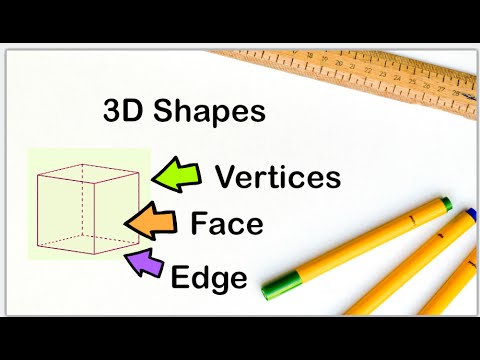
Denne side viser beviser for Euler formel : til enhver konveks polyeder, den nummer af hjørner og ansigter sammen er præcis to mere end nummer af kanter . Symbolsk V−E+F=2. Til eksempel, en tetraeder har fire hjørner , fire ansigter og seks kanter ; 4 - 6 + 4 =2.
Følgelig, hvad vil antallet af flader være, hvis der er 6 spidser og 12 kanter?
En terning eller en cuboid er en tredimensionel form, der har 12 kanter , 8 hjørner eller hjørner , og 6 ansigter.
Man kan også spørge, hvordan virker Eulers formel? Eulers formel , En af to vigtige matematiske sætninger af Leonhard Euler . Den første er en topologisk invarians (se topologi), der relaterer antallet af flader, hjørner og kanter af ethvert polyeder. Det skrives F + V = E + 2, hvor F er antallet af flader, V antallet af hjørner og E antallet af kanter.
hvad er formlen for forholdet mellem antallet af siders hjørner og kanter på en terning?
V - E + F = 2; eller med ord: den nummer af hjørner , minus nummer af kanter , plus antal ansigter , er lige til to.
Hvad er Eulers polyederformel?
Denne sætning involverer Eulers polyedriske formel (kaldes nogle gange Eulers formel ). I dag vil vi angive dette resultat som: Antallet af toppunkter V, flader F og kanter E i en konveks 3-dimensional polyeder , opfylder V + F - E = 2.
Anbefalede:
Hvad er fordelen ved at bruge Alligationsberegninger ved sammensætning?

1) Når du vil beregne mængden af fortyndingsmiddel, der skal tilføjes til et allerede forberedt præparat med højere styrke for at danne en lavere styrke. 2) Til blanding af to produkter med forskellige styrker til dannelse af et produkt med en ønsket mellemstyrke
Hvad er antallet af hjemløse i Amerika 2019?

I 2019 boede der omkring 567.715 hjemløse i USA. Mens dette tal havde været støt faldende siden 2007, er det i de sidste to år begyndt at stige
Hvad er en ulempe ved at bruge kul som energikilde?

Den største ulempe ved kul er dets negative indvirkning på miljøet. Kulfyrede energianlæg er en vigtig kilde til luftforurening og drivhusgasemissioner. Ud over kulilte og tungmetaller som kviksølv frigiver brugen af kul svovldioxid, et skadeligt stof forbundet med sur regn
Hvad er den formel, som en organisation kan bruge til at finde sine mest værdifulde kunder?

Hvad er den formel, som en organisation kan bruge til at finde sine mest værdifulde kunder? RFM - rapportering, funktioner, pengeværdi. RFM - rapportering, frekvens, markedsandel. RFM - seneste, frekvens, pengeværdi
Hvor mange nummererede flåder er der, og hvad er deres ansvarsområder?

Den amerikanske flåde har i øjeblikket syv aktive nummererede flåder. Forskellige andre flåder har eksisteret, men er ikke aktive i øjeblikket. Den første flåde eksisterede efter Anden Verdenskrig fra 1947, men blev omdesignet til tredje flåde i begyndelsen af 1973
